Theoretische Einleitung Zusammenhangsmaße

Wenn Sie den Zusammenhang zwischen zwei Variablen X und Y untersuchen möchten, ist es ein erster wichtiger Schritt die Daten in einer sinnvollen Form anzuordnen. Eine übersichtliche Darstellung der Daten erfolgt in einer Kreuztabelle.
Diese hat folgende allgemeine Form:

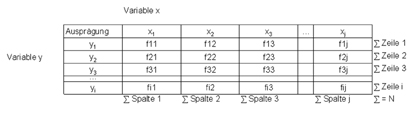
Die Variable X wird dabei in den Spalten abgetragen (x1, x2,?cxi), die Variable Y  in den Zeilen (y1, y2,?c,yi).
Es gilt: eine Kreuztabelle hat die Form r *c. Dabei steht r für "row" (engl. Zeile) und c für "column" (engl. Spalte).
Demnach sind beispielsweise folgende Formate möglich: 2x2-Kreuztabelle, 4x3-Kreuztabelle, 5x7-Kreuztabelle

Die allgemeine Bezeichnung der einzelnen Felder lautet fij. Diese setzt sich folgendermaßen zusammen:
die erste Zahl (Bezeichnung i) bezieht sich auf die Y-Variable, d.h. die Zeilenposition, die zweite (Bezeichnung j) auf die X-Variable, d.h. die Spaltenposition.
Ein Beispiel: f23 bezeichnet das Feld in der zweiten Zeile, dritte Spalte

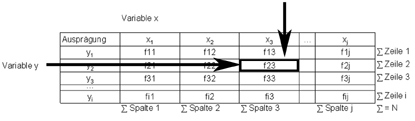
Für einige der nachfolgenden Zusammenhangsmaße ist es notwendig, die Randsummen zu berechnen.
Um die Randsumme für Zeile 1 zu berechnen werden alle Felder der ersten Zeile addiert,
 d.h. f11 + f12 + f13 +... + f1j oder kürzer ausgedrückt:

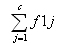
Um die Randsumme für die Spalte 1  zu berechnen werden alle Felder der ersten Spalte addiert,
d.h. f11 + f21 + f31 +...+ fi1 oder kürzer ausgedrückt

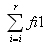
Die Summe aller Zeilen und aller Spalten ergibt die Anzahl der Gesamtfälle = N