Erstellung von Kreuztabellen

Die Vorgehensweise, wie eine Kreuztabelle erstellt wird möchten wir Ihnen an dieser Stelle anhand eine Beispiels verdeutlichen.

Eine Kindergartengruppe besteht aus insgesamt 20 Kindern (N=20), die Hälfte sind Jungen, die Hälfte Mädchen. Die Kinder wurden gefragt, ob sie lieber mit Lego oder mit Puppen spielen. Die Antworten (= empirische Verteilung) der Kinder sehen Sie in nachfolgender Abbildung:

Man kann erkennen, dass die Gruppe aus insgesamt 10 Mädchen (50%) und 10 Jungen (50%) besteht, wobei insgesamt 12 Kinder (60%) angeben, dass sie am liebsten mit Lego spielen und 8 Kinder (40%) geben an, dass sie Puppen bevorzugen.

Die Erstellung der theoretische Verteilung basiert auf folgender Annahme:
Wenn kein Zusammenhang zwischen diesen Variablen (Geschlecht des Kindes und Lieblingsspielzeug) besteht, dann dürfte es nur vom Zufall abhängen, ob z.B. ein Junge lieber mit Lego oder Puppen spielt.

Konkret gehen Sie bitte folgendermaßen vor:
Bilden Sie eine Tabelle mit gleicher Anzahl an Zeilen und Spalten wie in der empirischen Verteilung. Übernehmen Sie die Randhäufigkeiten der Zeilen und Spalten.

Es gilt:

• Die Gesamtanzahl der Kinder, die Jungen sind beträgt 10.
• Die Gesamtanzahl der Kinder, die am liebsten mit Lego spielen beträgt 12.

Es müssten also (10*12)/N  (N= Gesamtanzahl Kinder, hier: N=20) = (10*12)/20 = 6 Jungen angeben, dass sie am liebsten mit Lego spielen
D.h.: Um die theoretische Verteilung für die einzelnen Felder zu erstellen multipliziert man die entsprechenden Randhäufigkeiten und teilt diese durch die Gesamtanzahl N.

Die Zellen werden nun wie folgt berechnet:

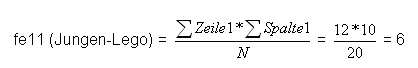
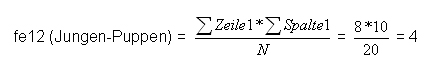
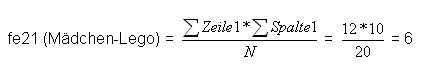
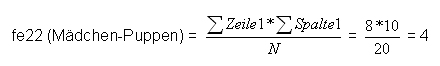
Übersichtlicher dargestellt ergibt sich für die theoretische Verteilung:

Oft kann es hilfreich sein, die theoretische Verteilung nicht in Form absoluter Zahlen, sondern als Anteile dazustellen. Dazu dividiert man die für die einzelnen Merkmale berechneten Anzahlen durch die Gesamtanzahl N. Es ergeben sich dabei folgende Anteile:

Nun wird die theoretische Verteilung mit der empirischen verglichen.

Dabei gilt:
Wird für Jungen, die mit Puppen spielen in der Realität der Kindergruppe (d.h. in der empirischen Verteilung) der Wert von 20% (der sich aus der theoretischen Verteilung ergibt, siehe oben) unterschritten (oder überschritten), dann tritt die Kombination dieser beiden Merkmale in der tatsächlichen (d.h. empirischen) Verteilung "überzufällig" selten (bzw. oft) auf.