Berechnung von Cramers V
Cramers V ist ein Kontingenzkoeffizient, der ebenfalls auf chi² basiert und immer zwischen 0 und 1 liegt. Es handelt sich um eine Maßzahl für die Stärke des Zusammenhangs zwischen zwei nominalskalierten Variablen wenn (mindestens) eine der beiden Variablen mehr als zwei Ausprägungen hat (z.B. 5x4-Tabelle, 2x3-Tabelle).
Bei einer 2x2-Tabelle kann man Cramers V zwar berechnen, man sollte jedoch Phi als Maßzahl verwenden.
Cramers V berechnet sich folgendermaßen:
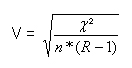
Mit:
n = Gesamtzahl der Fälle
R = der kleinere der beiden Werte: Anzahl Zeilen und Anzahl Spalten
Beispiel:

Um chi² zu berechnen muss wieder zuerst die Indifferenztabelle (= theoretische Verteilung) erzeugt werden. Die Felder werden dabei analog zur Berechnung der Felder bei Phi berechnet.
Beispiel: Feld links oben (Jungen - Lego)
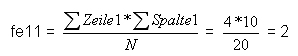
Es ergibt sich folgende theoretische Verteilung:

Dann kann chi² folgendermaßen berechnet werden:
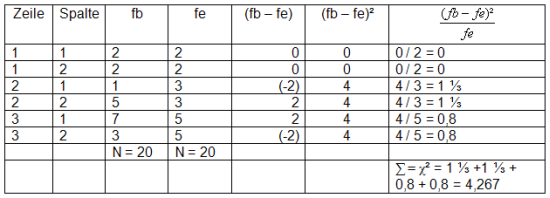
Mit
fb: Übernahme der Daten aus der empirischen Verteilung
fe: Übernahme der Daten aus der theoretischen Verteilung
Cramers V berechnet sich folgendermaßen:
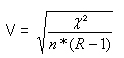
n = Gesamtzahl der Fälle - in unserem Fall: n = 20
R = der kleinere der beiden Werte: Anzahl Zeilen (hier 3) und Anzahl Spalten (hier 2) --> wähle Anzahl Spalten = 2
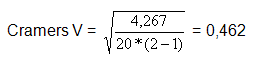
Interpretation
Cramers V liegt bei jeder Kreuztabelle - unabhängig von der Anzahl der Zeilen und Spalten - zwischen 0 und 1. Dieses Zusammenhangsmaß kann bei beliebig großen Kreuztabellen angewandt werden.
Cramers V = 0: es besteht kein Zusammenhang zwischen X (Geschlecht) und Y (Lieblingsspielzeug)
Cramers V = 1: es besteht ein perfekter Zusammenhang zwischen X und Y
Da Cramers V immer positiv ist, kann keine Aussage über die Richtung des Zusammenhangs getroffen werden.
In der Praxis findet man häufig folgende Interpretationen vor:
0,1 - 0,3 schwacher Zusammenhang
0,4 - 0,5 mittlerer Zusammenhang
> 0,5 starker Zusammenhang
Unser berechnetes Cramers V = 0,462 besagt, dass für das Beispiel ein mittelstarker Zusammenhang zwischen Geschlecht und Lieblingsspielzeug besteht.





