Varianzanalyse mit SPSS

Einfaktorielle Varianzanalyse:
Um zu entscheiden, ob sich Gruppen bezüglich einer Variable unterscheiden, benutzt man oft die so genannte einfaktorielle Varianzanalyse. Man findet sie im Menü „Analysieren“ unter dem Unterpunkt „Mittelwerte vergleichen“. Einfaktoriell heißt sie, weil nur eine Variable als Unterscheidungsmerkmal untersucht wird. Im Beispiel unten (Abb. 27) wird untersucht, ob der Schulabschluss der Teilnehmer einen Einfluss auf die Beurteilung der Qualität des Produktes A (QualiA) hat. In der Eingabemaske gibt man daher „QualiA“ als abhängige Variable und „Schulabschluss“ als Faktor (= unabhängige Variable) ein.

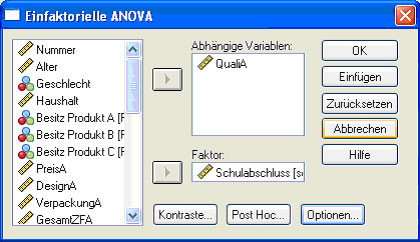
Abb.27

Mit Hilfe des Buttons "Optionen" kann nun eingestellt werden, welche zusätzlichen Kennzahlen ausgegeben werden, und ob ein Diagramm erstellt werden soll (Abb. 28).

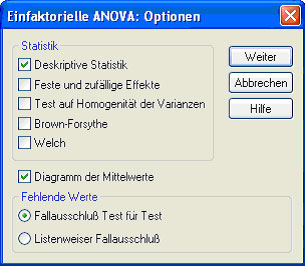
Abb.28

Die Ausgabe sieht folgendermaßen aus (Abb. 29): Die obere Tabelle gibt die angeforderten deskriptiven Kennzahlen für die einzelnen Gruppen an. Die zweite Tabelle ist der für die Interpretation wichtige Teil. Sie zeigt einen Signifikanzwert von 0,808, das heißt die einzelnen Gruppen (hier: Personen mit verschiedenen Schulabschlüssen) unterscheiden sich nicht hinsichtlich ihrer Bewertung der Qualität des Produktes.

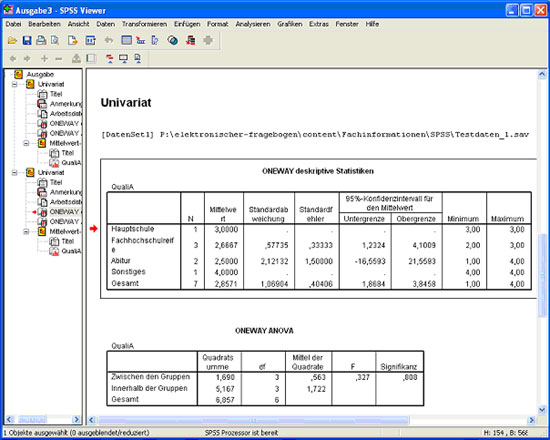
Abb.29

Univariate Varianzanalysen:
Möchte man den Einfluss mehrerer Faktoren prüfen reicht eine einfaktorielle Varianzanalyse nicht aus. Man muss Varianzanalysen durchführen, wie man sie unter dem Menüpunkt „Allgemeines lineares Modell“ findet.Wenn nur eine abhängige Variable betrachtet werden soll wählt man univariat. Möchte man nun in Ergänzung zum obigen Beispiel berechnen, wie es sich mit der Beurteilung der Qualität des Produktes B (QualiB) verhält, nicht nur unter Berücksichtigung des Schulabschlusses, sondern auch noch zusätzlich des Geschlechts, gibt man folgendes ein:

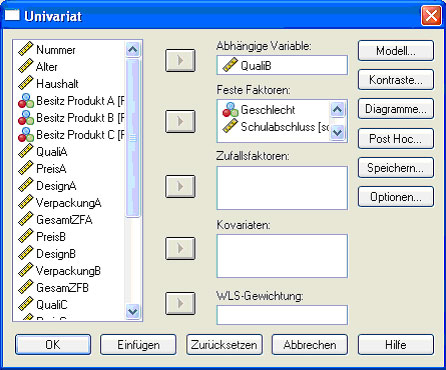
Abb.30

Im Ausgabefenster (Abb. 31) erfährt man nun zunächst unter „Zwischensubjektfaktoren", welche Gruppen für die einzelnen Faktoren existieren, d.h. wie groß die einzelnen Gruppen sind. Anschließend werden sowohl für beide einzelnen Faktoren, als auch für das Produkt (= die Interaktion) der Faktoren Tests durchgeführt. Anhand der Signifikanzwerte in der 3. und 4. Zeile der Tabelle „Tests der Zwischensubjektfaktoren“ sieht man, dass keine Unterschiede zwischen den Gruppen bestehen. Auch ein gemeinsamer Effekt (= Interaktion) von Schulausbildung und Geschlecht existiert nicht, wie man in der 5. Zeile sehen kann. Ein solcher gemeinsamer Effekt würde bedeuten, dass ein Faktor nur dann einen Einfluss hat, wenn eine bestimmte Ausprägung des anderen Faktors vorliegt, es ergäbe sich z.B. nur bei Abiturienten ein Geschlechtsunterschied.

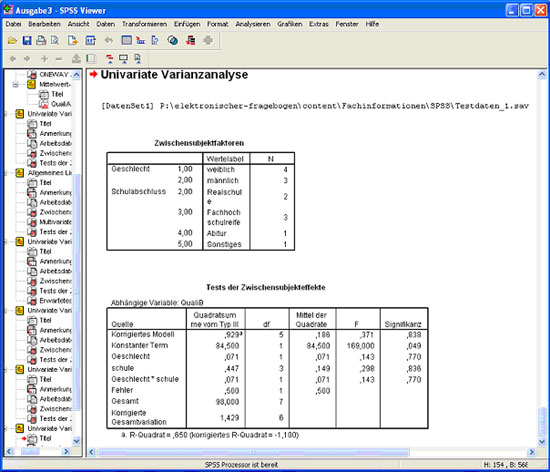
Abb.31

Multivariate Varianzanalyse:
Wenn man nun zusätzlich zur Qualität auch noch das Design mithilfe der unabhängigen Variablen Geschlecht und Schulabschluss vorhersagen möchte, wählt man unter „Analysieren“, „Allgemeines lineares Model“ „multivariat“ aus (Abb. 32). Die Eingabemaske sieht dann folgendermaßen aus:

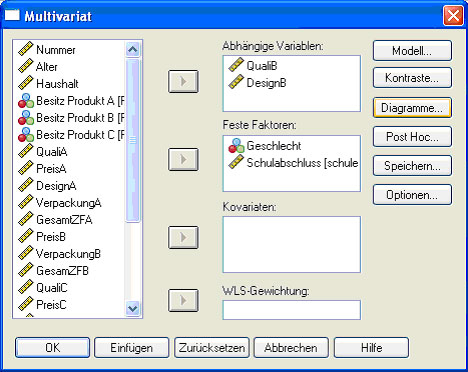
Abb.32

Man erhält folgende Ergebnisse im Ausgabefenster:

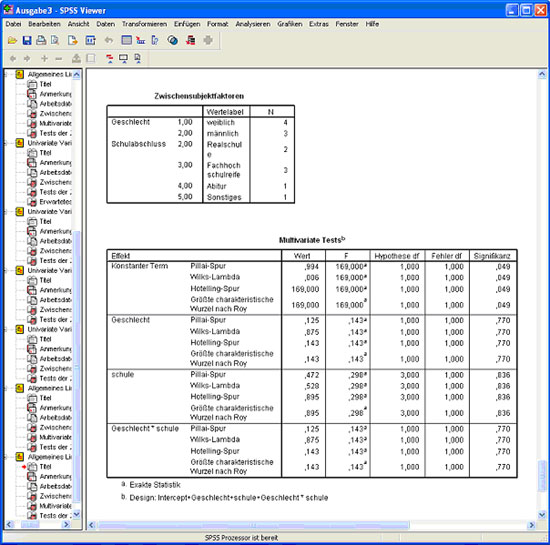
Abb.33

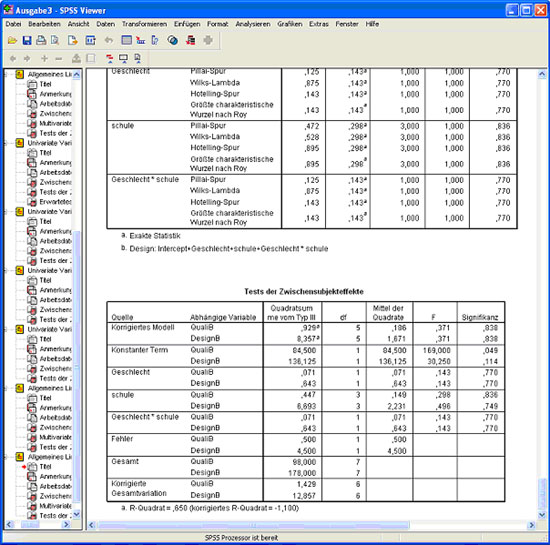
Abb.34

Wichtig ist dabei vor allem die letzte Tabelle "Test der Zwischensubjekteffetkte" (Abb. 34). Sie zeigt die Einflüsse der Faktoren (= unabhängige Variablen) auf die beiden abhängigen Variablen. Auch hier zeigen sich, wie die Signifikanzwerte deutlich machen, keine Unterschiede zwischen den verschiedenen Gruppen, d.h. weder die Bewertung der Qualität noch des Designs des Produktes hängt vom Geschlecht, der Schulbildung der Kunden oder der Interaktion der beiden Faktoren ab.