Regressionen berechnen mit SPSS

Mit Hilfe einer Regression versucht man (lineare) Vorhersageregeln für Variablen zu berechnen. Grundlage ist oft ein Modell aus mehreren hypothetischen Zusammenhängen. Man kann zwischen der einfachen und der multiplen hierarchischen Regression unterscheiden.

Einfache Regression:
Im ersten Fall werden alle Variablen, die zur Vorhersage genutzt werden sollen gleichzeitig berücksichtigt. Bei der multiplen hierarchischen Regression erfolgt dies in mehreren Schritten. Die entsprechenden Menüs befinden sich unter „Analysieren“, „Regression“ „linear“.
Zunächst wird die abhängige Variable, die man vorhersagen möchte, eingegeben. Bei der einfachen Regression (Abb. 20) gibt man anschließend alle Variablen unter „unabhängige Variable(n)“ ein.

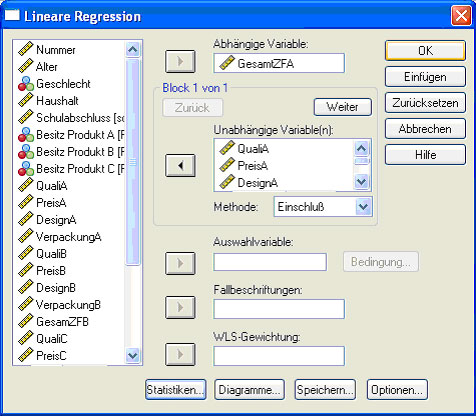
Abb.20

In diesem Beispiel soll überprüft werden, ob die Gesamtzufriedenheit mit dem Produkt A durch die Qualität, den Preis, das Design und die Verpackung des Produktes vorhergesagt werden kann. Man bekommt nun folgende Ausgaben:

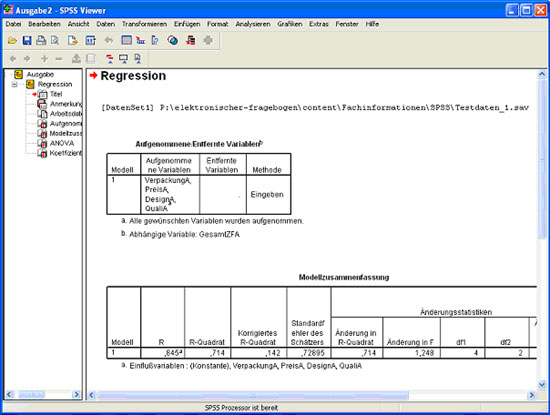
Abb.21

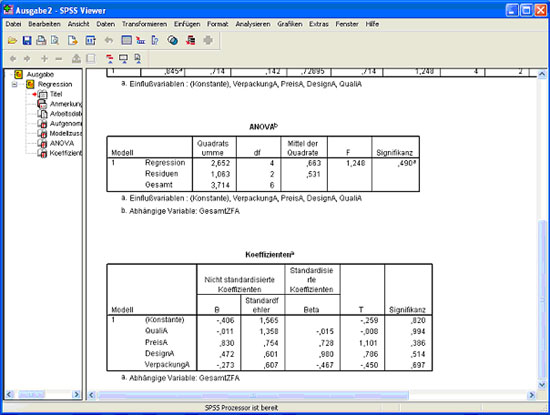
Abb.22

Im ersten Teil der Ausgabe (Abb. 21) erfährt man, welche Variablen benutzt wurden, anschließend sind allgemeine Informationen zum Modell aufgeführt. Hier interessiert besonders der Wert „Korrigiertes R-Quadrat“ (den man vorher bei lineare Regression (Abb. 20) unter Statistiken extra einstellen muss). Dies ist ein Maß dafür, wie viel Varianz der abhängigen Variable (Gesamtzufriedenheit) sich durch die unabhängigen Variablen (Qualität, Preis, Design und Verpackung des Produktes) erklären lässt. Der Wert für korrigiertes R² schwankt zwischen 0 und 1. Dabei gilt: je größer, desto besser. Im obigen Beispiel zeigt der Wert von 0,142 an, dass 14,2% der Varianz in Gesamtzufriedenheit durch Qualität, Preis, Design und Verpackung des Produktes erklärt werden, also recht wenig.
Im zweiten Abschnitt der Ausgabe (Abb. 22) unter der Überschrift ANOVA bekommt man das Ergebnis der Varianzanalyse für das Modell. Wichtig ist hier der Signifikanzwert. Er sagt, ob das Modell, d.h. die Kombination der unabhängigen Variablen, geeignet ist für die Vorhersage der abhängigen Variable. Der Wert sollte kleiner als 0,05 sein. Im obigen Beispiel liegt er deutlich darüber (0,490), das Modell ist also, wie schon durch die Statistik R² vermutet, ungeeignet um die Gesamtzufriedenheit eines Kunden vorherzusagen. In der untersten Tabelle (Abb. 22) erhält man Informationen über die Beiträge der einzelnen unabhängigen Variablen. Hier interessieren vor allem Beta und der Signifikanzwert. Beta macht eine Aussage über die Stärke und die Richtung des Zusammenhangs der einzelnen unabhängigen Variablen mit der abhängigen Variable. Im obigen Beispiel weist keine der unabhängigen Variablen einen signifikanten Zusammenhang mit der abhängigen Variable auf.

Multiple Regression:
Wie schon erwähnt kann man auch eine multiple hierarchische Regressionsanalyse durchführen. Hierfür gibt man im Auswahlmenü die unabhängigen Variablen schrittweise ein. Anstatt Qualität, Preis, Design und Verpackung in einem Schritt zu untersuchen kann man z.B. im ersten Schritt Preis und im zweiten Schritt Qualität eingeben. Zusätzliche Schritte können eingeführt werden, indem man über dem Fenster für die unabhängigen Variablen  auf „weiter“ klickt (Abb. 23), dadurch gelangt man dann in den nächsten Block. Die Variablen in einem Block werden gleichzeitig einberechnet, die einzelnen Blöcke werden dann der Reihenfolge entsprechend berücksichtigt.

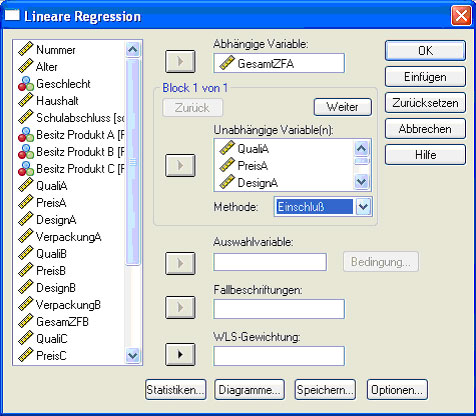
Abb.23

Um die wichtige Statistik „Änderung in R²“ zu erhalten ist es wichtig, dass man im Feld Multiple Regression (Abb. 23) unter dem Button Statistik die Änderung in R-Quadrat auswählt (Abb.24), damit man die einzelnen Schritte miteinander vergleichen kann.

Abb.24

Die Ausgabe für die hierarchische Regressionsanalyse sieht folgendermaßen aus:

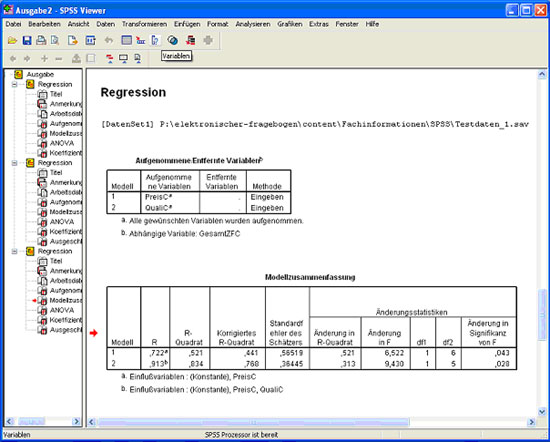
Abb.25

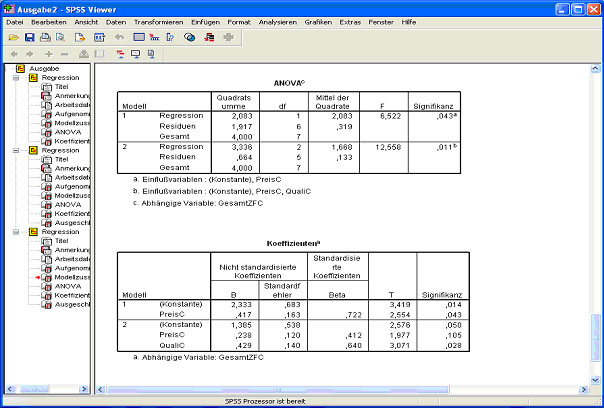
Abb.26

In der Tabelle Modellzusammenfassung (Abb. 25) erhält man die Werte für R-Quadrat, korrigiertes R² und Änderung in R². Dieses Mal werden zwei Modelle angezeigt, das erste Modell berücksichtigt dabei nur den ersten Schritt, das zweite Modell umfasst beide Schritte. Die Werte liegen bei 0,441 und 0,768 und sind damit deutlich besser als im ersten Beispiel. In der Tabelle ANOVA (Abb. 26) sieht man an den Signifikanzwerten von 0,043 und 0,011, dass beide Modelle gute Modelle sind, d.h. sie können Gesamtzufriedenheit erklären. In der letzten Spalte der Tabelle Modellzusammenfassung (Abb.25) sind die Signifikanzwerte für die Veränderung von einem Modell zum nächsten zu sehen. Der Wert von 0,028 für das zweite Model besagt, dass das zweite Modell signifikant besser ist als das erste. Das bedeutet Preis und Qualität zusammen sagen Gesamtzufriedenheit signifikant besser vorher als Preis alleine. In der letzten Tabelle (Abb. 26) sieht man wieder die Beta Werte für die unabhängigen Variablen. Im ersten Modell ist Preis signifikant (Beta = ,417, Signifikanz = ,043), das bedeutet der Preis hängt mit der Gesamtzufriedenheit zusammen. Im zweiten Modell wird zusätzlich Qualität berücksichtigt. Hierbei sieht man, dass Preis nicht mehr signifikant wird (Beta = ,238, Signifikanz = ,105), d.h. der Preis scheint keine Rolle mehr zu spielen, wenn man die Qualität berücksichtigt.